Written by Makram Merdas, Consultant,
and François-Xavier Duqué, Principal Consultant.
Introduction
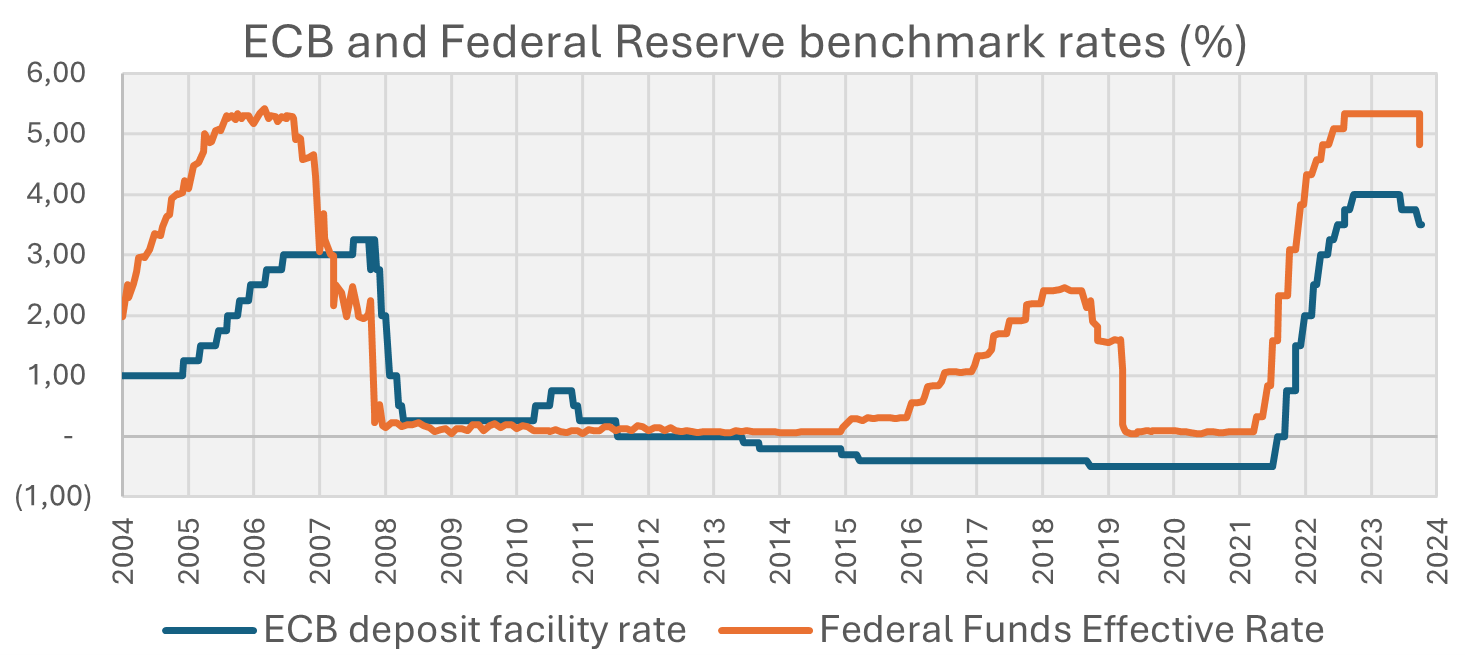
The recent rise in interest rates, following a long period of record lows, has been the fastest in decades. The ECB and the FED are now starting to decrease policy rates. Amid geopolitical tensions and economic uncertainties, a volatile interest rate market is likely to persist for an extended period. This will require banks to be cautious and proactive in managing their interest rate positions. While many banks have benefited from the increase in interest rates, a reversal of the tide could prove damaging if interest rate exposures are not well managed and hedged.
This article provides first a brief overview of the regulatory and organisational framework used by banks to manage the interest rate risk associated with banking activities. The article then proceeds to discuss the conventional measurement tools and explore various techniques and strategies used to manage and hedge a bank’s interest rate risk.
The ALM Function and the ALCO
The IRRBB and ALM frameworks are key in navigating the uncertainties associated with the interest rate risk.
The so-called banking book houses the bank’s traditional intermediation activities - as taking deposits and granting loans – and is structurally exposed to interest rate volatility. The regulatory framework that handles this risk is the “interest rate risk in the banking book” (IRRBB) standards. It refers to the current or prospective risk to the bank’s capital and earnings, arising from adverse movements in interest rates. Fluctuations in interest rates change the economic value (EV) of the bank, because they affect the timing, the size and the discounting of the cash flows, whether on its assets, liabilities, or off-balance sheet instruments. Changes in interest rate also affect the bank’s earnings or profitability by altering the income and expenses constituting the bank’s so-called net interest income (NII).
Asset and Liability Management (ALM) covers a broader spectrum and refers to the practice of managing financial risks that arise from mismatches of asset and liabilities. In addition to interest rate risk management, ALM also deals with liquidity management and optimizing the balance sheet in terms of the bank’s funding strategy or asset allocation.
Although banks differ in their organization, the ALM function is often responsible for managing IRRBB. At its head, the Asset and Liability Committee (ALCO) brings together the treasury, risk and finance departments, and possibly business lines managers. Its primary task is to establish and ensure the application of the ALM policy. In the context of IRRBB, the ALCO sets targets and limits for the key metrics based on the bank’s risk appetite, and more broadly ensures that the bank is compliant with the IRRBB regulatory requirements, as briefly exposed below.
Regulatory Landscape
Basel Committee on Banking Supervision (BCBS)
IRRBB is part of Pillar 2 in the Basel capital framework. Basel Committee issued a set of principles in 2004 and updated them in 2016.
The Basel standards are concerned with properly identifying interest rate risks and distinguishes three main sub-types. Gap risk (also known as repricing risk) occurs when interest rate-sensitive assets and liabilities reprice or mature at different times. For example, a long-term fixed-rate mortgage loans funded by short-term deposits. Basis Risk arises from the imperfect correlation between changes in interest rates for financial instruments that have similar tenors but are priced using different interest rate indices or references. For example, a floating-rate asset priced off Libor funded by a floating-rate liability priced off the ESTR overnight index. Optionality Risk can be either behavioural, as in loans that can be prepaid or deposits that can be withdrawn, or automatic, such as in caps and floors provisions.
Under the Basel standards, IRRBB should be measured with both economic value and earnings metrics across an appropriate range of interest rate shocks and stress scenarios. Banks must disclose the impact of specific regulatory scenarios on their EV and NII. The Supervisory Outlier Test (SOT) compares the bank’s maximum change in economic value of equity (ΔEVE) under these scenarios with 15% of its Tier 1 Capital.
The Basel standards also provide guidelines for IRRBB governance, risk appetite statement, measurement systems, modelling techniques, modelling assumptions, capital adequacy as well as the details of a standardized framework that banks can use, either voluntarily or on the orders of supervisory authorities.
European Banking Authority (EBA)
In October 2022, the European Banking Authority (EBA) published its guidelines on the management of IRRBB and CSRBB, building on the guidelines published in 2018 and 2015. Concomitantly, the EBA published regulatory technical standards (RTS) on the standardised methodology and the supervisory outlier test. Most of these regulations are consistent with BCBS standards but provide a greater level of detail. The RTS introduces a new SOT on NII, where the initial threshold—maximum ΔNII not exceeding 2.5% of Tier 1 Capital— has eventually been raised to 5% in an updated version.
IRRBB Measurement Techniques
Repricing Gap
The most straightforward way to assess IRRBB is to build a repricing gap. It involves the bucketing of all notional amounts items on predefined (regulatory or internal) tenors according to their maturity date (for fixed-rate instruments) or their repricing date (for floating instruments). Notional amounts are signed positively or negatively for assets and liability respectively. The resulting net gap position can be used to approximate the NII impact of future interest rate changes under a constant balance sheet assumption:
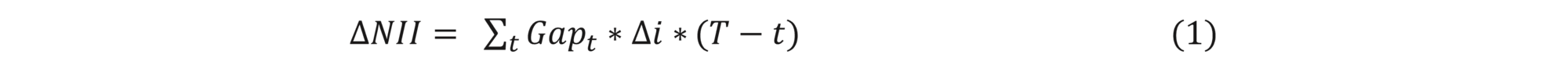
Where ∆i is the interest rate shock and T is the time in years to the end of the NII window (typically 1 year), while t is the time in years to the middle point of a given bucket.
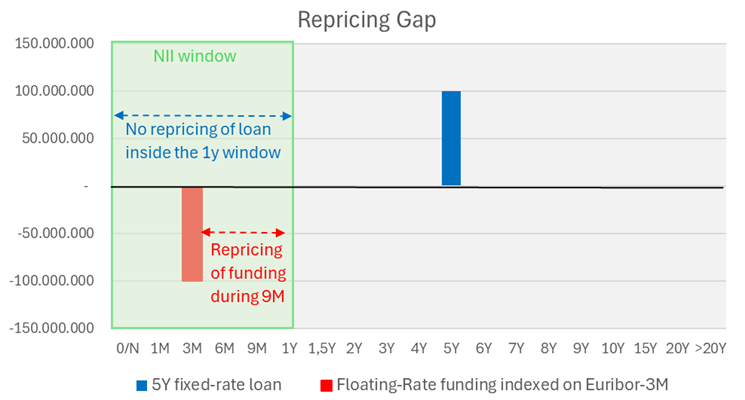
Figure: Repricing gap for a simple balance sheet where 5Y loans are funded by floating-rate liabilities indexed on Euribor-3M
This ∆NII estimate is crude because it ignores possible changes in the size of the gaps that may arise when the bank or the client’s behaviour adjusts to changes in the interest rate environment. Possible difference in “pass-through” rates through time and between products or changes in the commercial margins are also ignored.
Economic value impacts (∆EVE) can be estimated by discounting the gaps under different rate curves. But this approach cuts many corners and proper price value of a basis point (PV01), duration or scenario analysis are better suited.
Sensitivity Analysis
Sensitivity analysis, often referred to as PV01 or DV01 analysis, is a technique that quantifies the change in the present value of cash flows resulting from a 1 basis point shift in the yield curve, either as a parallel move, or ideally bucket by bucket. To this end, all instruments should be revalued before and after the shock, including their optional components.
The PV01 metric can also be “sliced” by reference rate, giving a complementary view on the basis risk that may exist in terms of EV when assets and liabilities are priced or discounted on different rate curves.
This representation is useful to have a quick grasp of the tenors (and possibly reference rates) to which the bank is most sensitive. But it has the drawback of being a “local” measure, as the 1bp shock does not show possible changes in behaviour that may occur under a larger stress. Hence, the PV01 analysis is sometimes complemented by a convexity (or curvature) metric that captures possible changes in PV01 in response to interest rate shocks. Scenario analysis is a more comprehensive way of capturing non-linear effects.
Duration Analysis
Duration is a popular alternative sensitivity metric. It can be understood in two complementary ways. Macaulay duration only applies to fixed cash flow instruments and is defined as the weighted average time until repayment, typically measured in years:
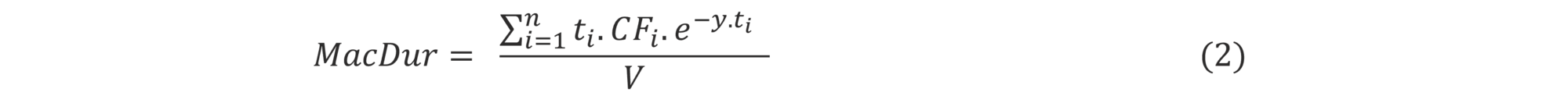
As the formula suggests, times to repayments (ti) are weighted by the present values of the cash flow (CFi) as a proportion of the present value of all cash flows (V), using the yield-to-maturity (y) as the discount rate.
More generally, the duration of any instrument can also be understood as (minus) the relative change in price for a parallel shift in yields. This is the so-called modified duration:
The Macaulay duration and the modified duration are strictly identical for fixed cash flow instruments when the yield is continuously compounded as in formula (1), The modified duration provides an intuitive way of assessing the relative sensitivity of an instruments to absolute fluctuations in interest rates. Indeed equation (3) can be reordered as:
For example, a bond with a duration of 7 years will approximatively lose 7% (in relative terms) when the rate increase by 1% (in absolute terms). Replacing ∆y by 1bp in equation (3), we find:
Hence, the duration analysis is a variation of the PV01 sensitivity analysis that has an intuitive underpinning (as the weighted average time to repayment). Duration analysis helps banks manage interest rate risk and is often a metric of choice to define the risk appetite statement or set limits at the ALCO. The metric suffers from the same limitations as the PV01 metric (it measures the exposure to small parallel shifts in the yield curve).
Scenario analysis
A more general way of assessing the interest rate risk is to simulate changes in economic value (∆EVE) or earnings (∆NII) under a variety of internal and regulatory scenarios. This allows a bank to identify the circumstances under which it is vulnerable and address them effectively.
Regulatory scenarios consist in specific parallel up/down, flattening/steepening and short up/down shocks, while internal scenarios can be historical interest rate shocks or custom scenarios that reflect a bank’s risk profile. Economic scenarios involving larger shocks allow the capture of non-linear effects associated with changes in behaviour or other optionalities. For NII scenarios, sophisticated banks will include in their repricing models’ expectations about pass-through rates and commercial margins product by product.
Behavioural Modelling
The quality of both EV and NII scenario critically depends on the quality of the modelling of the behavioural features. In a declining interest rate environment, borrowers will be more likely to prepay and refinance their loans (as the termination penalty is often limited by law), whereas in a rising interest rate environment, clients may withdraw some of the cash held in deposit or saving accounts in favour of more profitable investments. Early redemption of term deposits also becomes more common. Such behaviours can lead to swings in capital and earnings if not well managed.
Non-Maturity Deposits
Non-Maturity Deposits (NMDs) are deposits - typically on sight and saving accounts - that clients can withdraw at short notice and on which banks can unilaterally change the remuneration. Although funds can be withdrawn overnight, in practice, these deposits exhibit stickiness and significant duration. Given the importance of deposits as a source of funding, assessing this duration adequately is key to managing the overall IRRBB.
As a preliminary, regulators encourage separating stable from non-stable deposits and impose isolating core deposits. Under the voluntary standardised framework, stable deposits are the portion unlikely to be withdrawn with a high degree of likelihood. Core deposits are then the portion of the stable deposits that is found not to reprice in response to changes in market rates (no quick “pass-through” to client rates). Non-stable and non-core deposits are treated as short term positions (usually overnight), while core duration is modelled separately.
Simple approaches to assess deposit stability are based on a statistical analysis of historical volumes, looking at the largest volume declines at a given horizon and confidence level. Ideally, the analysis should be done at vintage level to carve out the effect of new business arising from new clients (as the EV has to be calculated under a run-off assumption). A cruder approach is to look at the evolution of volumes per client.
More sophisticated approaches aim at modelling the joint evolution of volumes and deposit rates, possibly also taking macro-economic factors into account, while avoiding the usual econometric pitfalls (see our article here for a presentation of such models).
Different routes are open to banks to model the core deposits. A classical approach is to identify an optimal replicating portfolio, which is the combination of fixed income instruments that most closely reproduces the deposit cash flows. The sensitivity of the replicating portfolio is then used as a proxy for the core deposits in EV calculations. Such analyses used to be based on historical volumes and deposits rates only. But regulators are encouraging banks to include a forward-looking perspective and consider the expected performance of the replicating portfolio under a wide range of interest rates scenarios, which also requires the modelling of deposit rates (and possibly volumes) under these scenarios.
Another route is to assess the pass-through of changes in markets rates to the deposit rates (i.e. “deposit betas”) and imply the repricing profile of core deposits from these pass-through rates. Partial equilibrium models (also called error correction mechanisms) work well in this respect but alternative techniques as PCA or ARIMA can also be used. These pass-through rates will also be used to model NMD’s repricing in NII simulations (under a constant balance sheet hypothesis for regulatory reports).
It is important to note that segmentation of customers (such as jurisdiction, product type, currency, characteristics of the depositor) plays critical role to capture the behavioural factors. Sophisticated AI and machine learning methods can be used to achieve a correct segmentation.
Prepayment Risk
Prepayment occurs when clients make unscheduled payments on a fixed-rate loan before its contractual maturity, reducing the principal and altering the expected cash flows and duration of the loan. Prepayment is driven either by financial incentives, such as refinancing a current loan at a lower rate, or non-financial incentives, such as unexpected needs by customers or strategic decisions by firms. Usually, a penalty applies when a client prepays a loan; prepayment risk arises when the amount of the penalty charged by the bank does not fully offset the loss in interest income.
To manage this risk, future prepayments on fixed-rate loans should be estimated under different market conditions. The Conditional Prepayment Rate (CPR) is the most used to model prepayment in a portfolio. The simplest approach is a static model, which generates a constant prepayment rate based on historical data unconditional on market interest rate levels. However, dynamic approaches can also be applied, taking into account market rates and refinancing incentives. As in NMDs modelling, it is important to segment the analysis by types of prepayable products, currency, jurisdiction, and borrowers’ characteristics to ensure a reliable estimation.
IRRBB Management and Hedging
After identifying and measuring interest rate risk, the next step for a bank is to manage its IRRBB and possibly hedge it when risk appetite limits are under threat.
Natural hedging can be achieved by acquiring assets that match the funding structure or adjusting the funding structure to match the assets, for example by issuing long-term bonds to fund long-dated assets. But the bank’s intermediation model (transforming short term deposits into longer term loans) often limits its ability to close the interest rate gaps naturally and other means are needed.
Derivatives such as interest rate swaps, swaptions, forward rate agreements, or forward bonds are commonly used by banks to close EV and NII exposures. The hedging strategy needs to be tailored to specific objectives and aims to achieve a target profile (target gap or sensitivity metrics). For example, if a bank is funding long-term fixed-rate assets with short-term floating-rate deposits, entering long-term fixed-rate payer swaps with matching maturities will close the repricing gap and secure its net interest margin.
Figure: Case of a simple balance sheet where 5Y loans are funded by 3M-floating-rate liabilities. Impact of hedging with a 5Y swap receiving 3M floating and paying fixed.
Types of hedges
A first distinction is made between cash flow hedges and fair value hedges. In the IRRBB context cash flow hedges aim at reducing the variability of cash flows that arises from volatile interest rates. They are typically associated with floating-rate exposures. In contrast, fair value hedges are used to mitigate changes in the fair value (or economic value) of fixed-rate exposures.
A second distinction exists between micro hedging and macro hedging. Micro Hedging is a method used to mitigate risk on a single item within a larger portfolio and it requires a nearly perfect correspondence between the hedged item and the hedging instrument. Macro Hedging in contrast aims at mitigating the risk of a portfolio of items that are inconvenient to hedge individually, such as retail loans and deposits. Both methods can be used to reduce volatility in NII or EVE and maintain them below the targeted limits under different scenarios.
Some residual risk may remain due to basis risk or discounting differences, even with micro hedges. Hedge effectiveness testing is conducted to assess the extent to which changes in the fair value or cash flows of the hedged item are offset by the hedging instrument. When linear hedges are used (swaps, futures), hedge effectiveness may be diminished by the existence of optional features. For example, prepayment or early redemption may create unanticipated changes in cash flows, potentially resulting in over hedging. Employing a dynamic hedging strategy, which involves frequent rebalancing of the hedge relationship, can help prevent over-hedging. A “layered” hedging approach can also be applied, where a portion of the portfolio that is unlikely to be affected by prepayment is defined as the hedged item.
Hedge Accounting
In the absence of proper accounting arrangements, hedging is likely to create instability in the financial statements. Indeed, banking book instruments - like deposits and loans - are typically accounted at amortised cost so that gains or losses associated with changing interest rates will accrue through time. In contrast, changes in the fair value of derivatives will flow to profit-and-loss accounts immediately as they arise.
Hedge accounting is a response to this problem. It is an optional technique that modifies the recognition of gains and losses (or revenues and expenses) on hedging instruments and hedged items, so that both are recognised in P&L (or OCI) in the same accounting period:
- For fair value hedges, the change in the fair value of the hedged item that can be attributed to the hedge risk is taken into PnL with the derivative (e.g. via the hypothetical derivative method). The net residual PnL then reflects the ineffectiveness of the hedge.
- For cash flow hedges, gains or losses on the effective portion of the derivative are recognized in OCI (as cash flow hedge reserve), while the ineffective portion remains in PnL.
IAS 39 defines the requirements for hedge accounting since 2018. However, institutions can opt to continue following IFRS 9 rules. Both frameworks define requirements in terms of effectiveness testing and documentation for the hedging relationship to be valid. It is worth noting that the European Commission passed some “carve-out” provisions in 2005 allowing EU banks to continue using fair value hedge accounting for derivatives hedging core deposits.
Enhance your IRRBB Management
In volatile markets, banks must adopt a proactive approach to identify, measure and manage IRRBB risks, keeping NII and EVE within the regulatory and internal limits. A crucial step is to properly identify the sources of gap, basis and option risks on and off the balance sheet. Behavioural modelling plays an important role in understanding the bank’s exposure and quantifying IRRBB risks properly in adapted sensitivity and scenario analyses. When risk appetite limits are under threat and natural hedging falls short, the bank may need to engage in micro or macro hedging strategies, taking the accounting implications into considerations. All these elements need to be organised within a strong governance framework under the lead of the ALCO committee.
Amid these challenges and the increasing importance of IRRBB, our expert team is ready to help you achieve your IRRBB goals, enhancing your ALM practices, from identifying and measuring IRRBB risks to implementing effective hedging strategies or improving IRRBB governance.
Reference
1. The credit spread risk of banking book (CSRBB) is a risk that is related to IRRBB and pertains to changes in market perception about the broad credit quality of instruments. Basel standards already require the Identification and monitoring of CSRBB; the EBA guidelines detail these requirements further.
2. When the yield is compounded k times a year, the relationship becomes: MacDur=ModDur.(1+y/k)